Относительность траектории | ТМ 1938-12

З. ЭМИ, Рисунки Н. ЕЛИЗАРОВА

Из окна вагона быстро мчащегося поезда вы роняете камень. Вы видите, что он упал вертикально вниз, как это и должно быть, если тело свободно падает.

А что увидит наблюдатель, стоящий на полотне железной дороги? Он будет утверждать, что камень описал в пространстве кривую линию — параболу.

Кому же из вас верить?

Всякого, кто склонен поверить второму наблюдателю, мы принуждены разочаровать: какой-нибудь третий наблюдатель, находящийся на Солнце, дал бы совершенно иное описание траектории камня. Он утверждал бы, что камень полетел по прямой, параллельно земной орбите.

В самом деле, «солнечный» наблюдатель видит перемещение земного шара в пространстве, а вместе с ним и камня (остальные движения камня ничтожно малы). Скорость движения Земли вокруг Солнца равна почти 30 км в секунду, причем отрезки земной орбиты должны казаться с Солнца прямыми линиями.

Быть может, читатель готов уже признать правильным утверждение третьего наблюдателя? Послушаем в таком случае, что скажет четвертый, помещающийся «над» центром Галактики — нашей звездной системы. Он сообщит, что камень описал дугу, и притом со скоростью 275 км в секунду: с такой именно скоростью обращается вся солнечная система вокруг центра Галактики.

Если бы мы спросили бесконечное число наблюдателей, находящихся на самолетах, на Луне, Марсе, различных звездах и т. д., какую траекторию описал камень, мы получили бы бесконечное число противоречивых ответов. Кто же из всех наблюдателей прав?

Из окна вагона быстро мчащегося поезда вы уронили камень. Вы видите, что он упал вертикально вниз.

А наблюдатель, стоящий на полотне железной дороги, будет утверждать, что камень описал в пространстве кривую линию — параболу.

Ясно, что каждый из них прав по-своему: все дело в «классическом принципе относительности», с которым читатель встречался уже на страницах нашего журнала («Парадоксы принципа относительности» в № 5«Техника — молодежи»).

А вот другой случай. Вообразим, что ваш поезд мчится с чудовищной скоростью — 500 м в секунду. На расстоянии 500 м от него параллельно движется с точно такой же скоростью другой поезд. На крыше одного из вагонов второго поезда, напротив вашего вагона, укреплена мишень. Вы стреляете в нее из ружья и попадаете в цель. Скорость полета пули равна 500 м в секунду. В каком направлении летела пуля?

Для вас — в направлении, перпендикулярном движению поездов. Однако снимок, сделанный сверху, с мачты столба, показал бы, что пуля летела по прямой линии, пересекающей направление движения поездов под углом в 45°. Почему именно в 45°, понятно: относительно неподвижного фотоаппарата пуля передвигалась с одинаковой скоростью не только по направлению к мишени, но и вместе с поездом. Почему же в таком случае траектория камня, выпавшего из окна вагона, не прямая, а парабола? И что это за кривая — парабола?

Таким видит направление пули человек, стреляющий с мчащегося поезда в мишень, которая движется с такой же скоростью.

Снимок, сделанный сверху, с мачты столба, показал бы, что пуля летела по прямой линии, пересекающей направление движения поездов под углом в 45°.

Тут мы сталкиваемся с «методом координат» известного французского философа и математика Рене Декарта (1596 — 1650 гг.). Этот метод дал возможность исследовать различные кривые, которые до этого изучить было нельзя.

В чем же заключается метод координат Декарта? Положение точки рассматривается относительно какой-то выбранной системы. Простейшей из таких систем является прямоугольная система координат на плоскости — «декартова система». Она состоит из двух взаимно перпендикулярных пересекающихся прямых линий — «осей координат».

Горизонтальная ось называется «осью абсцисс», вертикальная — «осью ординат», а точка их пересечения — «началом координат». Если известны расстояния какой-либо точки от каждой из осей — ее «координаты», — то тем самым положение точки на плоскости строго определено. Горизонтальная координата точки называется «абсциссой», а вертикальная — «ординатой».

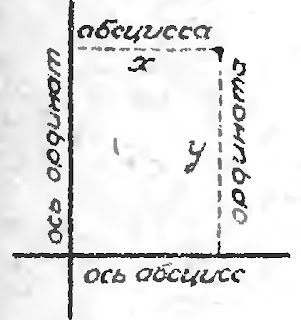Декартова система координат.

Математически простейшую параболу изображают таким квадратным уравнением: \(x=y^2\). Буквой \(x\) обозначена длина абсциссы любой точки параболы, а буквой \(y\) — длина ординаты той же точки. Если, например, \(y=2\), то \(x=2^2=4\); при \(y=3\) абсцисса \(x=3^2=9\) и т. д.

Теперь нам станет ясно, почему камень описал именно параболу. Ведь он двигался одновременно в двух направлениях: вместе с поездом в горизонтальном (ось абсцисс) и под действием силы тяжести — в вертикальном (ось ординат). Горизонтальное движение — равномерное, а вертикальное — равноускоренное (о земном ускорении \(g\), равном 9,8 м/сек³, упоминалось в № 4«Техника—молодежи», в статье «Всемирное тяготение»). При ускоренном движении длина пути, пройденного телом, равна \(\frac{gt^2}2\), где \(t\) — время в секундах.

Итак, длина вертикальною пути камня пропорциональна квадрату времени, горизонтального же — первой степени времени. Следовательно, зависимость между обоими движениями камня — квадратная, типа \(x=y^2\). Вот почему наблюдателю. стоявшему на земле, казалось, что камень описал параболу. Ведь он следил за падением камня в неподвижном (относительно Земли) системе координат. А в этой системе камень совершал два движения: равномерное горизонтальное и равноускоренное вертикальное. Отсюда и получилась параболическая форма траектории. По той же причине по отношению к Земле имеет параболическую форму траектория тела, брошенного в любом направлении, кроме вертикального. Поэтому параболическую форму имеет траектория артиллерийского снаряда, струи воды, пушенной из брандспойта, и т. д.

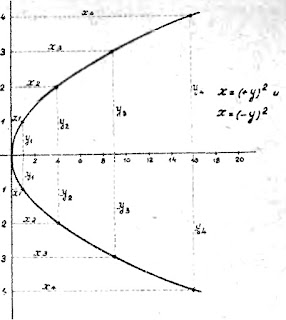Математически простейшую параболу изображают квадратным уравнением: \(x=y^2\). Буквой \(x\) обозначена длина абсциссы любой точки параболы, а буквой \(y\) длина ординаты той же точки.

Различные формы параболических траекторий тел (при отсутствии сопротивления воздуха).

Но почему же вы видели из окна вагона, что камень упал вертикально? Вяжется ли это с системой координат? Да. Сама система, в которой мы наблюдали падение камня (поезд), двигалась вперед с такой же скоростью, что и камень. Следовательно, в этой системе горизонтальная скорость камня равнялась нулю, и, значит, он двигался только в одном направлении — по оси ординат, вертикально.

Итак, форма траектории движущегося тела относительна. Так, например, греческий астроном Птолемей рассматривал движение небесных тел относительно системы, в начале координат которой находится Земля.

Земля кажется в этой системе неподвижной, а весь мир — вращающимся. Таким он и представляется земным обитателям. А великий астроном Коперник, показавший, что не Солнце вращается вокруг Земли, а наоборот, поместил в начало координат Солнце. Таким образом, в коперниковой системе координат Солнце неподвижно. В действительности же оно движется: Солнце обращается вокруг центра Галактики, совершая полный оборот в 224 млн. лет. Следовательно, можно рассматривать движение тел в системе координат начало которой находится в центре Галактики.

Если с Солнца наблюдать траекторию движения камня, то она покажется прямой линией, параллельной орбите земного шара.

Если центром системы принимается Солнце, Земля обращается вокруг Солнца по эллипсу (почти кругу), Луна же совершает в этой системе уже не одно, а два основных движения: почти круговое около Земли и вместе с Землей — сложное вокруг Солнца.

Тут мы сталкиваемся с относительностью масштабов. Скорость обращения Луны вокруг Земли равна примерно 1 км в секунду, а Земли вокруг Солнца — 30 км и секунду. Полный оборот вокруг

Земли Луна совершает примерно в 27 суток, а Земля вокруг Солнца — примерно в 365 суток. Среднее расстояние между Землей и Солнцем равно 149,5 млн. км, а между Луной и Землей — почти в 400 раз меньше, т. е. 384,4 тыс. км. Следовательно, в то время как Земля совершает один оборот вокруг Солнца, Луна успевает обойти Землю более 13 раз. Поэтому путь Луны вокруг Солнца представляет собой волнистую пинию, изогнутую в виде круга.

Вычертим орбиту Луны вокруг Солнца в правильном масштабе. Если масштаб выбрать так, что радиус земной орбиты равен 38,8 мм, то расстояние между Землей и Луной будет равно 0,1 мм. Эта величина настолько мала, что на чертеже совершенно незаметна. Масштаб как бы «съел» орбиту Луны вокруг Земли... Поэтому при малом масштабе путь Луны в коперниковой системе сольется с орбитой Земли, т е. будет представлять собой круг. В центре этого круга будет находиться Солнце.

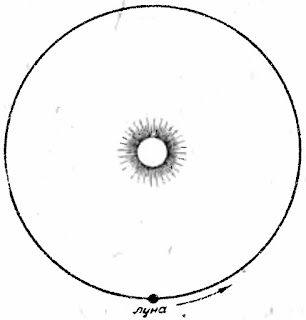При малом масштабе путь Луны в коперниковой системе координат сольется с орбитой Земли, т. е. будет представлять собой круг. В центре этого круга будет находиться Солнце.

В заключение заметим, что система Земля—Луна представляет собой единственный случай двойной планеты в солнечной системе. Так как размеры Земли и Луны сравнимы (диаметр Луны всего в 3,68 раза меньше диаметра Земли), то глазам наблюдателей, попавших, например, на Венеру, представилась бы эффектная картина: пара как бы танцующих в пространстве звездочек.

Статья дополнена до оригинального объема. Огромное спасибо каналу "Техника–молодёжи"