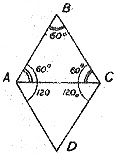
Такой — единственный — случай возможен. Если две равные силы приложены в одной точке тела под углом в \(120°\), сумма их равна одной из сил. Действительно, \(AC\) есть равнодействующая двух сил: \(AB\) и \(AD\), приложенных под углом в \(120°\). Но \(AC\) — это диагональ ромба. Из геометрии известно, что диагональ ромба делит углы, через которые она проходит, пополам, т. е.
\(\_BAC=\_BCA=\frac{120^\circ}2=60^\circ\).
Но так как сумма углов треугольника равна \(180°\), то \(\_ABC=60^\circ\). А против равных углов в треугольнике лежат равные стороны, — значит
\(AB\) = \(AD\) = \(AC\).






Комментариев нет:
Отправить комментарий