Кривая короче прямой

Наметив мелом две точки на классной доске, учительница предлагает юному школьнику задачу:

— Начертите кратчайший путь между обеими точками.

Подумав, ученик старательно выводит между ними запутанно-извилистую линию.

— Вот так кратчайший путь! —  удивляется учительница. — Кто тебя так научил?

— Мой папа. Он шофер такси.

Чертеж наивного школьника, конечно, анекдотичен; но разве не улыбнулись бы вы, если бы вам сказали, что дуга на рис. 1 есть самый короткий путь от мыса Доброй Надежды до южной оконечности Австралии? Или что начерченная на морской карте дуга есть кратчайший путь между Гамбургом и Нью-Йорком? Еще поразительнее следующее утверждение: изображенный на рис. 3 огромный кружный путь из Японии к Панамскому каналу короче прямой линии, проведенной между ними на той же карте!

Рис. 1. На морской карте кратчайший путь от мыса Доброй Надежды до южной оконечности Австралии обозначается не прямой линий, а кривой

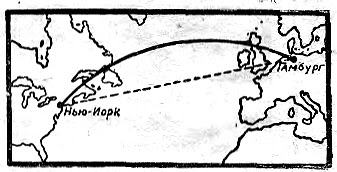Рис. 3. На этой морской карте кратчайший путь из Гамбурга в Нью-Йорк обозначается кривой линией

Рис. 4. Кажется невероятным, что путь по дугообразной линии, соединяющий на морской карте Иокогаму с Панамским каналом, короче прямой линии, проведенной между ними

Все это похоже на шутку, а между тем перед вами бесспорные истины, хорошо известные картографам.

Для разъяснения, вопроса нам придется сказать несколько слов о картах вообще и о морских в частности. Изображение на бумаге частей земной поверхности — дело непростое даже в принципе, потому что Земля — шар, а известно, что никакую часть шаровой поверхности нельзя развернуть на плоскости без складок и разрывов. Поневоле приходится мириться с неизбежными искажениями на картах. Придумано много способов черчения карт, но все они не свободны от этого недостатка: на одних имеются искажения одного рода, на других иного рода, но карт вовсе без искажений — нет.

Моряки пользуются картами, начерченными по способу старинного основателя научной картографии, Меркатора. Способ этот называется «меркаторской проекцией». Узнать морскую карту легко по ее характерной прямоугольной сетке: меридианы изображены на ней в виде ряда параллельных прямых линий; круги широты — тоже прямыми линиями, перпендикулярными к первым.

Вообразите теперь, что требуется найти кратчайший путь от одного океанского порта до другого, лежашего на той же параллели. На океане все пути доступны, и осуществить там путешествие по кратчайшему направлению всегда возможно, если знать, как оно пролегает. В нашем случае естественно думать, что кратчайший путь идет вдоль той параллели, на которой лежат оба порта: ведь на карте это — прямая линия, а что может быть короче прямого пути? Но мы ошибаемся: путь по параллели вовсе не кратчайший.

В самом деле: на поверхность шара кратчайшее расстояние между двумя точками есть соединяющая их дуга большого круга. «Большим кругом» на поверхности шара называется каждый круг, центр которого совпадает с центром этого шара. Все остальные круги на шаре называются «малыми». Но параллельный крут — малый круг. Дуга большого круга менее искривлена, чем дуга любого малого круга, проведенного через те же две точки; большему радиусу отвечает меньшая кривизна. Натяните на глобусе нить между нашими двумя точками, вы убедитесь, что она вовсе не ляжет вдоль параллели. Натянутая нить — бесспорный указатель кратчайшего пути, а если она на глобусе не совпадает с параллелью, то и на морской карте кратчайший путь не обозначается прямой линией: вспомним, что параллельные круги изображаются прямыми линиями, всякая же линия, не совпадающая с прямой, есть кривая. После сказанного становится понятным, почему кратчайший путь на морской карте изображается не прямой, а кривой линией.

Рис. 2. Простой способ разыскать с помощью глобуса кратчайший путь между двумя пунктами. Рисунок показывает между прочим, что кратчайший путь ведет иной раз через полюс

Рассказывают, что при выборе направления для Октябрьской (тогда Николаевской) железной дороги велись нескончаемые споры о том, по какому пути ее проложить. Конец спорам положило вмешательство царя Николая I, который решил задачу буквально «прямолинейно»: соединил Ленинград с Москвой по линейке. Если бы это было сделано на меркаторской карте, получилась бы конфузная неожиданность: вместо прямой дорога вышла бы кривой.

Вооружившись ниткой и имея под руками глобус, вы легко можете проверить правильность наших чертежей, убедиться, что дуги больших кругов действительно пролегают так, как показано на чертежах. Изображенный на рис. 1 будто бы прямой путь из Африки в Австралию составляет 6 020 миль, а «кривой» — 5 450 миль, т. е. короче на 570 миль, или на 1 050 километров. «Прямой» на карте путь из Лондона в Шанхай перерезает Каспийское море, между тем как действительно кратчайший путь пролегает к северу от Ленинграда. Понятно, какие со всем этим связаны потери времени и пережог угля.

Если в эпоху парусного судоходства не всегда дорожили временем, то с появлением паровых судов приходится платить за каждую излишне израсходованную тонну угля. Вот почему в наши дни ведут суда по действительно кратчайшему пути, пользуясь нередко картами, выполненными не в меркаторской, а в так называемой «центральной» проекции: на этих картах дуги больших кругов изображаются прямыми линиями.

Почему же прежние мореплаватели пользовались столь обманчивыми картами и избирали невыгодные пути? Ошибочно думать, что в старину не знали о сейчас указанной особенности морских карт. Дело объясняется, конечно, не этим, а тем, что карты, начерченные по способу Меркатора, обладают, наряду с неудобствами, весьма ценными для моряков выгодами. Такая карта, во-первых, изображает отдельные небольшие части земной поверхности без искажения, сохраняя углы контура. Этому не мешает то, что с удалением от экватора все контуры заметно растягиваются. В высших широтах растяжение так значительно, что морская карта вкушает человеку, незнакомому с ее особенностями, совершенно ложное представление об истинной величине материков: Гренландия кажется такой же величины, как Африка, Аляска больше Австралии, хотя Гренландия в 15 раз меньше Африки, а Аляска вместе с Гренландией вдвое меньше Австралии. Но моряка, хорошо знакомого с этими особенностями карты, они не могут ввести в заблуждение. Он мирится с ними, тем более, что в небольших участках морская карта дает точное подобие натуры.

Рис. 5. Морская или меркаторская карта земного шара. Она сильно преувеличивает размеры контуров, удаленных от экваторов

Зато морская карта весьма облегчает решение задач штурманской практики. Это единственный род карт, на которых путь корабля, идущего постоянным курсом, изображается прямой линией. Идти постоянный курсом значит держаться неизменно одного направления, одного определения «румба», иначе говоря, идти так, чтобы все меридианы пересекать под равными углами. Но этот путь может обозначаться прямой линией только на такой карте, на которой все меридианы — прямые линии, параллельные друг другу. А так как на земном кругу широты пересекаются с меридианами под прямыми углами, то на такой карте и круги широты должны быть прямыми линиями, перпендикулярными к линиям меридианов. Короче сказать, мы приходим к той именно сетке, которая составляет характерную особенность морской карты.

Пристрастие моряков к картам Меркатора теперь понятно. Желая определить курс, какого надо держаться, идя к назначенному порту, штурман прикладывает линейку к конечным точкам пути и измеряет угол, составляемый ею с меридианами. Держась все время в открытом море этого направления, штурман безошибочно доведет судно до цели.

Я. ПЕРЕЛЬМАН