КОДЫ ЗОЛОТОЙ ПРОПОРЦИИ, или Системы счисления для ЭВМ будущего?..

Как известно, информационной и арифметической основой современных компьютеров является двоичная система счисления. Ее изобретение приписывают китайскому императору Фо Ги, жившему в IV тысячелетии до н. э.

В европейской математике двоичный способ представления чисел, по-видимому, впервые описан итальянским математиком XIII века Леонардо Пизанским, прозванным Фибоначчи. Сын пизанского купца, получивший образование в арабских учебных заведениях, хорошо знакомый с алгеброй и десятичной системой счисления — достижениями арабской и индийской научной мысли, он в 1202 году написал «Книгу о счете», сыгравшую заметную роль в развитии математики в Западной Европе. В ней рассматривается ряд новых комбинаторных задач, наиболее известная среди которых — «о размножении кроликов». Решая ее, автор открывает математическую последовательность, известную под названием ряда Фибоначчи: 1, 1, 2, 3, 5, 8, 13. 21, 34, 55...

Нетрудно заметить, что каждый последующий член этого ряда, начиная с третьего, равен сумме двух предыдущих членов. И если обозначить 𝑛-й член через φ(𝑛), то его связь с предыдущими членами φ(𝑛-1) и φ(𝑛-2) выразится формулой: φ(𝑛) = φ(𝑛-1) + φ(𝑛-2).

Подобные соотношения, получившие название «рекуррентных» (от латинского «recurro» — «возвращаться»), стали мощным подспорьем в решении комбинаторных задач.

Теперь образуем числовой ряд, состоящий из отношений соседних чи-

сел Фибоначчи: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8... Легко показать, что предел этой последовательности совпадает со знаменитым числом 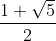 , характеризующим так называемую золотую пропорцию, или, как еще говорят, гармоническое, или золотое сечение.

Был ли известен столь замечательный математический факт связи чисел Фибоначчи с золотым сечением самому автору чисел? В его сочинениях никаких упоминаний об этом не обнаружено.

...Что же побудило Фибоначчи заниматься двоичной системой счисления? Анализ «Книги о счете» показывает, что собственно система счисления его интересовала мало. Иное дело — практические нужды торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16... (которую мы также назовем «двоичной» и возьмем в кавычки).

Взвешивание надо начинать с самой тяжелой из всех гирь, имеющихся в нашем распоряжении (разумеется, мы не рассматриваем тот случай, когда опытный продавец «на глазок» определяет вес товара, а затем с помощью гирь лишь окончательно уточняет его). Дальнейшие действия таковы. Если гиря тяжелее груза (то есть весы, которые могут принимать положение либо 0, либо 1, оказываются в положении 0), то ее надо заменить другой, ближайшей по весу. А если легче (положение 1) — оставить и добавить также следующую. Процедура продолжается до тех пор, пока не будет использована самая мелкая гиря. В результате получим, что товар весом, скажем, в 13 кг можно уравновесить таким вот набором «двоичных» гирь: 16 кг — 0; 8 кг — 1; 4 кг — 1; 2 кг — 0; 1 кг — 1. И если теперь условимся всегда считывать результат именно в таком порядке — сначала тяжелые гири, затем более легкие, вес груза можно указать в двоичном коде: 01101.

Вернемся теперь к задаче о золотом сечении отрезка, известной со школы также под названием задачи о делении отрезка в крайнем и среднем отношении — ее решение приведено на 4-й стр. обложки. Свойства золотого сечения — оно описывается уравнением 𝒳² - 𝒳 - 1 = 0, равного , создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.

Золотое сечение являлось своего рода жемчужиной пифагорейского учения о числовой гармонии мира. Позже принципы золотого сечения легли в основу композиционного построения многих произведений мирового искусства, начиная с архитектуры античности.

Вся древнегреческая культура развивалась под знаком золотой пропорции. Греки первые установили: пропорции хорошо сложенного человеческого тела подчиняются ее законам, что особенно хорошо видно на примере античных статуй (Аполлон Бельведерский, Венера Милосская). Фригийские гробницы и античный Парфенон, театр Диониса в Афинах — все они исполнены гармонии золотой пропорции.

В эпоху Ренессанса золотая пропорция возводится в ранг главного эстетического принципа. Леонардо да Винчи, Рафаэль, Микеланджело, Тициан и другие великие художники Возрождения компонуют свои полотна, сознательно используя золотое сечение. Нидерландский композитор XV века Якоб Обрехт широко использует золотое сечение в своих музыкальных композициях, которые до сих пор уподобляют «кафедральному собору, созданному гениальным архитектором».

В XIX веке уже не художники, а ученые-экспериментаторы, изучавшие закономерности филлотаксиса (расположения цветков), вновь обратились к золотой пропорции. Оказалось, что цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках и т. д. «упакованы» по логарифмическим спиралям, завивающимся навстречу друг другу. При этом числа «правых» и «левых» спиралей всегда относятся друг к другу как соседние числа Фибоначчи (13:8, 21:13, 34:21, 55:34). А ведь

это отношение в пределе дает нам золотую пропорцию!

В наши дни интерес к числам Фибоначчи и золотому сечению возродился с новой силой. В целом ряде музыковедческих работ подчеркивается наличие золотого еечения в композиции произведений Баха, Шопена, Бетховена. Сергей Эйзенштейн использует золотое сечение при монтаже эпизодов своих кинокартин. Академик Г. В. Церетели обнаруживает, что гармония стиха в поэме Шота Руставели «Витязь в тигровой шкуре» подчиняется золотому сечению *...

Наряду с прикладными исследованиями ученые продолжают активно развивать теорию чисел Фибоначчи и золотого сечения. Советский математик Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта. Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.

Одним из последних достижений в этой области является и открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений.

Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд гирь 1, 2, 4, 8, 16... на первый взгляд совершенно разные.

Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой (2=1+1; 4=2+2...), во втором — это сумма двух предыдущх чисел (2=1 + 1, 3=2+1, 5=3+2...). Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи? А может быть, эта формула даст нам новые числовые множества, обладающие какими-то новыми уникальными свойствами?

Действительно, зададимся числовым параметром 𝒮, который может принимать любые значения: 0, 1, 2, 3, 4, 5... И рассмотрим числовой ряд, 𝒮+1 первых членов которого — единицы, а каждый из последующих равен сумме двух членов: предыдущего и отстоящего от предыдущего на 𝒮 шагов. Теперь, если 𝑛-й член этого ряда мы обозначим через φₛ(𝑛), то получим искомую общую формулу: φₛ(𝑛) = φₛ(𝑛-1) + φₛ(𝑛-𝒮-1).

Очевидно, что при 𝒮 = 0 из этой формулы мы получим «двоичный» ряд, при 𝒮=1 — ряд Фибоначчи, при 𝒮 = 2, 3, 4... новые ряды чисел, которые получили название 𝒮-чисел Фибоначчи.

К этим-то 𝒮-числам Фибоначчи мы с харьковским математиком И. В. Витенько и пришли в 1964 году, когда решали описанную Фибоначчи задачу о наилучшей системе гирь, но в более общем случае — с учетом так называемого «принципа асимметрии измерения».

Что такое обобщенные золотые сечения, называемые также золотыми 𝒮-сечениями? Снова обратимся к рисункам на 4-й стр. обложки. Отрезок АВ разбит точкой С так, что .

Так вот, золотая 𝒮-пропорции есть положительный корень уравнения золотого 𝒮-сечения: 𝒳ˢ⁺¹ - 𝒳ˢ - 1 = 0.

Нетрудно показать, что при 𝒮 = 0 получается деление отрезка пополам, а при 𝒮=1 — уже знакомое классическое золотое сечение!

Выше мы установили математическую связь между золотым сечением и числами Фибоначчи. Возможно, нечто подобное существует между 𝒮-числами Фибоначчи и золотыми 𝒮-сечениями? И действительно, отношения соседних 𝒮-чисел Фибоначчи 𝛼ₛ с абсолютной математической точностью совпадают в пределе с золотыми S пропорциями! Математики в таких случаях говорят, что золотые 𝒮-сечения являются числовыми инвариантами 𝒮-чисел Фибоначчи.

В таком случае возникает правомерный вопрос: не обнаруживают ли себя числа 𝛼ₛ подобно тому, как это было, скажем, с числом 𝛼= 1,618, в каких-либо явлениях природы?

В статье профессора А. Соколова «Тайны золотого сечения» (см. «ТМ» № 5 за 1978 г.), научного руководителя лаборатории бионики МЭИ, высказывается интересная гипотеза о существовании некоторых числовых инвариантов, характеризующих волны электрической активности головного мозга. И действительно, физиологами, исследующими ритмы мозга, обнаружено, что инвариант главной волны бета равен 1,618. Инварианты других известных волн — дельта, тэта, альфа и гамма, — вычисляемые из значений их граничных частот и из уравнения золотого сечения (применительно к данному явлению), равны 1,221; 1,324; 1,272 и 1,272. Инварианты волн альфа и гамма одинаковы — это подтверждают эксперименты. Последующие математические исследования всех известных волн электрической активности мозга позволили восстановить систему алгоритмов, которая предсказывает существование волн с инвариантами 1,464 и 1,3801

А инварианты волн мозга 1,618, 1,464, 1,380, 1,324 есть не что иное, как золотые 𝒮-сечения, соответствующие значениям 𝒮 = 1, 2, 3, 4!

Еще более удивительные факты, подтверждающие существование золотых 𝒮-сечений в природе, приводит белорусский философ Э. М. Сороко в книге «Структурная гармония систем» (Минск, «Наука и техника», 1984). Оказывается, например, что хорошо изученные двойные сплавы обладают особыми, ярко выраженными функциональными свойствами (устойчивы в термическом отношении, тверды, износостойки, устойчивы к окислению и т. п.) только в том случае, если удельные веса исходных компонентов связаны друг с другом одной из золотых 𝒮-пропорций. Это позволило автору выдвинуть смелую гипотезу: золотые 𝒮-сечения есть числовые инварианты не только мозга, но и любых самоорганизующихся систем. Будучи подтвержденной экспериментально, эта гипотеза (закон гармонии систем) может иметь фундаментальное значение для развития синергетики — новой области науки, изучающей процессы в самоорганизующихся системах.

...Теперь вновь обратимся к процедуре взвешивания, описанной Фибоначчи. Но на этот раз веса гирь выберем в соответствии с каким-либо 𝒮-рядом Фибоначчи, а не с «двоичным» рядом. Очевидно, что результат взвешивания можно будет записать в том же виде: есть гиря — нет гири того или иного веса. Но ведь вес груза выражается числом — значит, мы пришли к новому способу двоичного представления любых чисел. Это и есть 𝒮-коды Фибоначчи.

Скажем, взвешивая «Фибоначчиевыми» гирями вес в 15 кг, можно использовать такой их набор: 13 кг — I; 8 кг — 0; 5 кг — 0; 3 кг — 0; 2 кг — 1; 1 кг — 0; 1 кг — 0. Или такой: 8 кг —- 1; 5 кг — 1; 3 кг — 0; 2 кг — 1; 1 кг — 0; 1 кг — 0.

В коде Фибоначчи это запишется так: 1000100 или 110100. В этой неоднозначности и заключено главное свойство 𝒮-кодов Фибоначчи.

При 𝒮>0 они являются избыточными, поскольку каждому такому числу соответствует некоторое множество кодовых комбинаций, все элементы которого могут быть получены с помощью так называемых операций «свертки» и «развертки», представленных в виде 0 и 1 кода Фибоначчи. Не вдаваясь здесь в математические подробности этого процесса, отметим лишь, что денежные системы многих стран широко его используют. Так, начальный ряд монет, принятых в СССР, соответствует ряду Фибоначчи: 1, 2, 3..., а их размен (5=3+2, 3 = 2+1, 2=1 + 1) соответствует операциям «развертки» и «свертки» в коде Фибоначчи. Подчеркнем: подобно тому, как при денежных разменах сумма находящихся в обращении денег остается неизменной, так и при «свертке» и «развертке» двоичных разрядов не изменяется закодированное число.

Какое же практическое значение имеет обнаруженное свойство 𝒮-кодов Фибоначчи? Выполним все возможные операции «свертки». Получится кодовая комбинация с удивительным свойством — двух единиц в ней рядом не встретится! А если выполнить все операции «развертки»? Правильно: ни разу не обнаружится рядом двух нулей. В этом удивительном математическом свойстве просматривается могучее средство контроля и обнаружения отказов в будущих вычислительных структурах, работающих с использованием кода Фибоначчи. Ибо задача создания отказоустойчивых вычислительных систем сводится прежде всего к проблеме обнаружения отказов, что и обеспечивают коды Фибоначчи и золотой пропорции, являющиеся как бы естественным обобщением классического двоичного способа кодирования чисел. Общими у них оказываются лишь способы позиционной нумерации действительных чисел, причем при 𝒮 = 0 код золотой 𝒮-npoпорции и сводится к классическому двоичному коду.

Дальнейшим развитием способа явились коды золотой 𝒮-пропорции. С их помощью .можно выразить любое действительное число в виде суммы степеней золотых 𝒮-пропорций с двоичными коэффициентами 0 и 1.

Принципиальное отличие нового способа кодирования чисел заключается в том, что основания новых кодов, представляющие собой золотые 𝒮-пропорции, при 𝒮>0 оказываются иррациональными числами. Таким образом, новые системы счисления с иррациональными основаниями как бы ставят «с головы на ноги» исторически сложившуюся иерархию отношений между числами рациональными и иррациональными. Дело в том, что сначала были «открыты» числа натуральные; затем их отношения — числа рациональные. И лишь позже — после открытия пифагорейцами несоизмеримых отрезков — на свет появились иррациональные числа. Скажем, в десятичной, пятеричной, двоичной и других классических позиционных системах счисления в качестве своеобразной первоосновы были выбраны натуральные числа — 10, 5, 2, — из которых уже по определенным правилам конструировались все другие натуральные, а также рациональные и иррациональные (в пределе) числа.

Своего рода альтернативой существующим способам счисления выступает новая, иррациональная система, в качестве первоосновы, начала счисления которой выбрано иррациональное число (являющееся, напомним, корнем уравнения золотого сечения); через него уже выражаются другие действительные числа.

Вот как выглядит, скажем, число 5 в виде конечной суммы иррациональных чисел:

Еще раз подчеркнем: любое натуральное число всегда представимо в виде конечной — а не бесконечной, как думали ранее! — суммы степеней любой из золотых 𝒮-пропорций. Это одна из причин, почему «иррациональная» арифметика, обладая удивительной математической простотой и изяществом, как бы вобрала в себя лучшие качества классической двоичной и «Фибоначчиевой» арифметики. Вот почему она имеет огромное практическое значение в качестве системы счисления для ЭВМ будущего.

Сегодня ни у кого не вызывает сомнений тот факт, что одним из основных путей решения важнейшей проблемы современных ЭВМ — проблемы надежности — является введение избыточности. А введение избыточности с помощью кодов Фибоначчи и золотой пропорции обладает неоспоримыми преимуществами по сравнению с другими, применяемыми в настоящее время способами.

Во-первых, системы счисления с иррациональными основаниями являются естественным обобщением классической двоичной системы счисления, которую они включают в качестве частного случая. Они сохраняют в себе одно из важнейших достижений математической науки прошлого — позиционность счисления, а значит, и все преимущества классического двоичного счисления: простоту арифметических операций, «наглядность» кода, возможность сдвига кодов и представления чисел с «плавающей» запятой и др.

Во-вторых, за счет большой избыточности можно создать единую систему сквозного оперативного контроля всей (без исключения) цифровой аппаратуры, и в перспективе — создать отказоустойчивые компьютеры и другую цифровую технику.

Избыточность предлагаемых систем счисления уже используется для решения других задач цифровой техники, в частности для повышения плотности и достоверности цифровой магнитной записи-воспроизведения, а также для увеличения емкости и повышения достоверности хранения информации в запоминающих устройствах на цилиндрических магнитных доменах. Так, в Винницком политехническом институте уже создан 17-разрядный, работающий на кодах Фибопаччи, преобразователь — высокоточный, метрологически стабильный и быстродействующий. Есть все основания полагать, что эти качества в полной мере будут присущи и другим аналого-цифровым и цифро-аналоговым преобразователям, построенным с использованием нового принципа.

Отметим, наконец, что классическая двоичная арифметика, ныне используемая в вычислительной технике, обладает принципиальными недостатками: невозможно, например, выполнять арифметические действия последовательно, от старших разрядов к младшим, это резко снижает производительность ЭВМ. В компьютерах, которые будут работать с иррациональными системами счисления, эти «минусы» отсутствуют, поскольку в так называемой последовательной (поразрядной) арифметике математические операции можно выполнять начиная со старших разрядов.

Характерно, что новая высокопроизводительная арифметика и соответствующие ей арифметические узлы для нового поколения компьютеров могут найти применение в многопроцессорных вычислительных системах с программируемой архитектурой (А. В. Каляева).

Полученные результаты, несомненно, будут способствовать решительному повороту в воззрениях разработчиков ЭВМ от традиционных систем счисления к кодам Фибоначчи и золотой пропорции — системам счисления ЭВМ будущего.

* Изучая структуру произведения, ученый его решил «арифметизироватъ», то есть заменил каждое слово числом, равным количеству слогов в нем. Получился перевод поэмы на числовой язык. Анализируя этот перевод всех 6348 шестнадцатисложных строк, он обнаружил в изящных и звучных стихах золотое сечение, характеризующееся числами 3, 5 и 8.

* Любопытная деталь, лишний раз подтверждающая, что самые важные и полезные идеи носятся в воздухе. Когда А. П. Стахов в начале 1978 года готовил статью «Золотая пропорция в цифровой технике» для отраслевого журнала «Автоматика и вычислительная техника» (опубликована в № 1 за 1980 год, а первый вариант поступил в редакцию 4.7.1978 года), в которой впервые сформулировал свои идеи об использовании систем счисления с иррациональными основаниями в вычислительной технике, он еще не знал, что в том же, 1978 году издательство «Мир» выпускает в свет 3-й том монографии крупнейшего американского специалиста по программированию Д. Кнута «Искусство программирования для ЭВМ». И когда он прочел ее, то с удивлением обнаружил, что Кнут широко использовал методы Фибоначчи и золотого сечения для решения задач программирования. Там же и была найдена ссылка на статью американского ученого Джорджа Бергмана «Система счисления с иррациональным основанием», опубликованную в 1957 году, в которой описан хоть и частный, но весьма важный случай, когда основанием является классическая золотая пропорция. Хотя Стахов описал более общий класс таких систем, тем не менее первенство открытия «иррациональных систем счисления» принадлежит Джорджу Бергману, и в последующем варианте своей статьи он внес ссылку на его работу. Характерно, что инженеры просто не заметили статью Бергмана. Она была опубликована в специальном математическом журнале, а ее автор к тому же писал так: «Я не знаю ни одного практического использования подобных систем, кроме как для умственного упражнения и приятного времяпрепровождения, хотя они могут быть пригодны для теории чисел».